Controlling Light's Propagation by Light ?!

          Light is wave. Well, most of the time, it behaves like so. Due to its wave nature, it is not trivial to confine any light beam to its original shape when it is propagating except a plane wave. Putting in one sentence, light beams tend to diverge. Actually, even a plane wave has edges in reality, so plane waves diverge too. So, what if we can create a light beam that retains its diameter and energy distribution transverse to the direction of propagation through space, a “spatial soliton” as being called by scientific community, wouldn’t that be a great achievement? After all, human beings have been trying to manipulate light for thousands of years. In fact, we can do much more thanks to the efforts of researchers who are fascinated by making this happen.

          The way to do so is through “light-matter interaction”. With the advance of laser, we can now make the strength of the electric field high enough to affect material's property (refractive index, most of the time). That simply means that when strong light propagates in the material, it does not simply pass through it -- it interacts with the material. This kind of interaction modulates the material’s property (the change of the refractive index, for example). And this modulation in turn affects how light is propagating. With careful design, it is possible to have an equilibrium in which light propagates without changing its spatial shape. In other words, the modulation of the material’s property compromises the diffraction effect imposed by nature. This is like a real time feedback loop which can be pictured as that in the figure 1.

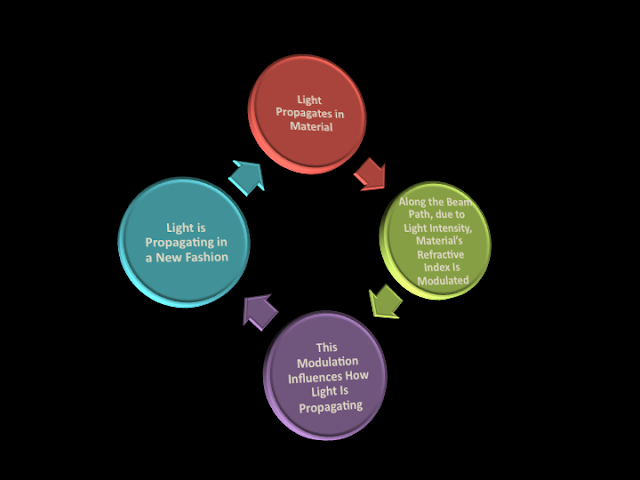Figure 1. The virtual feedback loop when strong light beam is propagating in the material.

          The first and foremost phenomenon nowadays is probably the self-focusing of a laser beam in some crystals. For example, when a laser beam is propagating inside Ti:Sapphire crystal, it makes the refractive index higher along its beam path due to laser intensity. This inhomogeneity of refractive index in turn focuses the laser beam. Without going to too much detail, this phenomenon is actually the basis for modern mode-lock lasers which you might easily find one in most universities.

          How about a few more fancy things!? When two light beams launched parallel inside the crystal (Sr0.6Ba0.4Nb2O6 crystal, for example), they can attract or repulse each other depending on their phase relationship. This is again due to that light beams are modifying the refractive index of the crystal, and this modification guides how light beams should propagate in real time. Light beams can even form a spiral pair if certain parameters are achieved. So they circle each other while propagating forward. Just like a DNA strand made by light beams (figure 2).

Figure 2. Light beam pairs propagate and spiral about each other in the crystal. This graph is at courtesy of George I. Stegeman and Mordechai Segev in Science 286 1518 (1999)

          Researchers like Professor Mordechai (Moti) Segev have pushed the limit one step further by employing external light sources in the feedback loop (figure 3). In brief, pairs of plane waves are mixed inside the crystal to create standing waves (constructive interference). The distribution of the energy modifies the refractive index of the crystal. As a result, a transient 2D photonic lattice/waveguide is formed (figure 4). Then the light is launched from the proper crystal surface. The light propagates and interacts with the “structured refractive index” such that the diffraction is suppressed. That is, it becomes a “spatial soliton” by the cooperation among itself, external light sources, and the crystal.

Figure 3. The virtual feedback loop when external light sources are used.

Figure 4. (a) Pairs of plane waves form standing waves inside the crystal. Red arrow indicates the direction of propagating light beam (b) The refractive index of the XY cross section in the crystal. Due to the distribution of the energy of standing waves, refractive index of the crystal is modulated (refractive index is higher when color is brighter). The graph is at courtesy of Jason W. Fleischer, Mordechai Segev, Nikolaos K. Efremidis, and Demetrios N. Christodoulides in Nature 422 13 147 (2003).

          The story gets better. Professor Segev utilized a phenomenon called “Anderson Localization” to confine light beam’s diameter. In a nutshell, “Anderson Localization” states that when the random disorder of the medium becomes substantial, the wave within it tends to be localized since all the outgoing diffractive waves interfere destructively. Consequently, the light does not diffract and remains spatially intact when propagating. Based on this principle, Professor Segev creates a photo-induced 2D photonic lattice (the way we mentioned above), superimposed with disorder (from another laser source), and launched the light through it. It is shown that the light is actually localized in 2D if certain disorder is reached (figure 5). Again, the interplay between light and material made this happen.

Figure 5. Anderson localization of light. The graph is courtesy of T. Schwartz, S. Fishman, G. Bartal, and M. Segev in Electronics Letter 443 3 165 (2008) and Nature 446 52 (2007).

          Before this article gets too long and boring, we should get some nanotechnology involved in this business. An interesting phenomenon called “Thermophoresis” is utilized to localize the light too. Thermophoresis states that the “temperature gradient” in the solution would change the distribution of the particles within it. If the particles tend to move from high/low temperature to low/high temperature, it is called “positive/negative” thermodiffusion. This is great weaponry for us if we want to localize light. Here is how it goes -- 20 nm diameter polystyrene (PS) particles were suspended in water solution, and the laser beam is propagating through it. Since the laser dissipates heat in the solution, along the beam path the temperature is higher. PS particles have “negative” thermodiffusion, so they will be more concentrated in the beam path (figure 6). In addition, PS particles have higher refractive index, so over all, refractive index is higher along the beam path. Just like self-focusing in the crystal, this inhomogeneity in refractive index will focus the light beam! This work is shown beautifully in a recent paper -- PRL 105, 163906 (2010).

          For details about all these, guess what!? Coming to CLEO for Professor Sergev’s planetary talk!

Figure 6. Thermopherisis can be used to localize light when light is propagating through the solution of PS particles. 

DISCLAIMER

The opinions expressed herein are those of the author and do not represent the Optical Society of America (OSA) or any OSA affiliate.